Chapter 1b

Essential of Geography

Geosystems, 4th Canadian ed (4CE)*, pp. 20-37 (top)  (Geosystems, 3rd Canadian ed (3CE)*, pp. 18-35 (top))

* Note that you may be using one of two editions of Geosystems:  for convenience I will use abbreviations:

  • if you have Geosystems, 4th Canadian edition 2016, I will use the abbreviation:  4CE (most of you will have this one)
  • if you have Geosystems, 3rd Canadian edition 2013, I will use the abbreviation:  3CE

 “The earth is the Lord’s, and everything in it.   The world and all its people belong to him.  He built the earth’s foundation on the seas and built it on the ocean depths.”

Psalm 24:1-2 

“O Lord, let me feel this world as Your love taking form,  then my love will help it.”

– prayer of Indian Christian leader, Rabindranath Tagore (d. 1941)

There is a video version of this lecture here:  https://youtu.be/WA4ddA4FSHI. 

The exam is based on the content in these notes, so please print them off to study from.

I.  The Earth’s Shape

The earth, of course, is a perfectly round sphere!  Right?  Wrong!

Actually the Earth is an “oblate ellipsoid”; it’s a sphere that is compressed at the poles and bulges at the equator.  This is due to the centrifugal force of the earth spinning on its axis.  This means that if you were to go around the Earth, it is actually shorter to go up and over the poles rather tan around the equator!

  • See 4CE Figure 1.12, p. 20 (3CE, Figure 1.11 p. 17)  – Earth’s Dimensions

How do we know the earth is roughly spherical (before satellites, etc.)?  Folks as far back as Pythagoras (c. 540 BC) and Aristotle (384-322 BC) believed it was!  Why?

  1. the “sinking ship syndrome” – as a ship sails away it appears to sink below the waves.  This is because the ship is actually sailing over the surface of the earth, a sphere.  It disappears over the curve of the Earth. If the Earth were flat, the boat would simply get smaller and smaller, but not appear to  “sink.”
  2. lunar eclipses – when the earth passes directly between the sun and the moon, it’s shadow appears to cross the moon as an arc.  Only if the Earth were a sphere would it cast a circular shadow on the moon.
  3. Observation of the North Star (directly over the North Pole).  As you move south, the North Star gets lower and lower in the sky (closer to the horizon).  In fact, for every 111 km you travel, it appears to drop 1°.  If you work out the geometry (and the Greek, like Pythagoras, were good at geometry) this could only happen if the earth were spherical.

Isn’t it curious that the ancient Greeks had this all worked out!  But some medieval Christians believed the Earth was flat!  Many Christians in the middle-ages believed the Bible taught a three tiered universe:

  1. Heaven … above the Earth
  2. the Earth
  3. Hell … below the Earth

Because the Bible says, “The sun rises …” they were sure the Earth was the centre of the universe.  The sun went around the Earth.  Since this is literally what the Bible taught (in their interpretation), the Earth must be flat!  Their observation led to this as a logical conclusion.

Some Christians were horrified by suggestions the Earth might be spherical and NOT the center of the solar system … those were unbiblical assertions (in their opinion).  It threatened their view of biblical authority.  It threatened the foundations of their Christian faith.  (There still are churches that teach the earth is the centre of the universe and the solar system – while they may concede the earth is spherical, they would argue that the sun revolves around the earth / modern astronomy is all wrong – because the Bible, according to their interpretation, says so (Gerardus Bouw is the main proponent of this view)).

For some in the Medieval Church, one’s opinion about the shape of the Earth became a test of authentic Christian faith.  If you couldn’t believe the Bible that the Earth was flat and the centre of the universe, how could you believe it about anything!?!?  Faith in Christ was not the issue … the shape of the Earth and solar system was!  Many people believe folks like Copernicus and Galileo were accused of being heretical for challenging this conviction; in fact it was a bit more complicated – and political – than just that.  You can read more about Galileo’s conflict with the church here.

The problem was … what?

  • The problem was one of poor biblical exegesis and hermeneutics (interpreting what the Bible actually says and what it means today).  The Bible doesn’t actually say the Earth is flat in a definitive way (does it?).  Biblical writers described things as they appeared to be — the sun does appear to rise.  The winds appear to come from the “four corners” of the earth, but that is a figure of speech, isn’t it?  They were describing things as they saw them; they were not trying to make scientific observations.  It is our error, as interpreters, to think biblical writers are trying to give us modern scientific explanations when they are, in fact, simply telling things as they see them, using figures of speech, and are limited by the “scientific” understandings of their age.

This is a sobering reminder for us that, when it comes to issues of natural sciences and the Bible, we need to be careful about our exegesis and hermeneutics.  Otherwise we may ourselves using issues related to our interpretation of issues in science and the Bible (the age of the Earth?) as a test of orthodoxy (does the Bible actually say how old the Earth is? Not really …).  And we may find ourselves ignoring the real issues (faith in Christ).  And we may find ourselves in untenable scientific territory when the clear evidence contradicts what we interpret the Bible to be saying.  With a variety of issues, if we try to deuce scientific knowledge from the Bible,  it may well be our error, as interpreters, to think biblical writers are trying to give us modern scientific explanations when they are, in fact, simply telling things as they see them, using figures of speech, and are limited by the “scientific” understandings of their age.

II. How Big is the Earth?

In about 247 BC, Eratosthenes (the librarian at Alexandria, Egypt) observed that at noon, the sun was directly overhead (no shadows at all) at the city of Syrene, Egypt.  Meanwhile, in Alexandria, the sun came down at an angle, casting a shadow.

By calculating the angle of the sun and knowing the distance between the two cities, he calculated the circumference of the earth to be about 46,250 km.  Modern measurements calculate the circumference to be 40,008 km.  Not too bad!

A. Does the Earth Move?

Yes!  The Earth spins like a top on its axis, called rotation.  It takes about 24 hours for one complete rotation (one day!).  At the equator, a point on the earth’s surface is moving at about 1700 km/h.  At our latitude, we’re moving at about 650 km/h.  At the poles you do not move at all!

The earth’s rotation is responsible for:

  • our routine of day and night
  • tides (this course)
  • the curved flow paths of air and water (the Coriolis Effect, which we discuss in the other course

The Earth also revolves around the sun.  It takes approximately 365¼ days for one full revolution around the sun.  This, combined with the fact that the earth is tilted on its axis, is responsible for our seasons (also in the other course).

B. Locating Points On the Earth

In order to locate places on the earth, geographers from the days of the ancient Greeks onwards created grid systems.

Grid systems on spheres are related to these key terms and concepts:

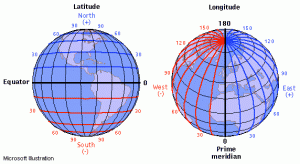
1. Longitude and Latitude

a. Latitude is the angular distance, measured in degrees, between any location and the Equator (0°).  It will range from 0° – 90° either North or South of the Equator.  90ºN is the north pole; 90ºS is the south pole. 4CE Figure 1.13, p. 20 (3CE Figure 1.13, p. 18) – Parallels of Latitude

Degrees are further subdivided into 60 minutes (‘); minutes are subdivided into 60 seconds (“).

  • e.g. Toronto, ON, is located at 43° 32′ N.  A specific neighborhood within Toronto can be located using minutes as well.
  • e.g. Moncton, NB, is located at 46º 7′ N.  A specific neighbourhood within Moncton could be located using minutes as well.
  • e.g. Vancouver, BC, is located at 49º 28′ N.  A specific neighbourhood within Vancouver could be located using minutes as well.
  • e.g. Regina, SK, is located at 50º 26′ N.  A specific neighbourhood within Regina could be located using minutes as well.

1b Lat_LongLatitude can be determined with reference to the sun or the stars.  You can measure the angle of the sun above the horizon at noon and calculate how far south or north you must be (the sun is higher in the sky at noon the further south you go).  Or you can measure the angle of the North Star (Polaris). Polaris always stays within 1 degree of celestial north pole. If a navigator measures the angle to Polaris and finds it to be 10 degrees from the horizon, then he is on a circle at about 10 degrees of geographic latitude. By using a sextant (which measures the angle the sun or North Star is above the horizon), you can figure out how far you are from the Equator.

b. Longitude is the angular distance, measured in degrees (°), between a  point and the Prime Meridian (0°).  It will range from 0° –  180° either East or West (whichever is shortest).  4CE Figure 1.16, p. 22 (3CE Figure 1.15, p. 20) – Meridians of Longitude

Degrees are further subdivided into 60 minutes (‘); minutes are subdivided into 60 seconds (“).

  • e.g. Moncton, NB, is located at 64º 41′ W.  A specific neighbourhood within Moncton could be located using minutes as well.
  • e.g. Toronto, ON, is located at 79°23′ W. A specific neighborhood within Toronto can be located using minutes as well.
  • e.g. Regina, SK, is located at 104° 40′ W.  A specific neighbourhood within Regina could be located using minutes as well.
  • e.g. Vancouver, BC, is located at 123° 12′ W.  A specific neighbourhood within Vancouver could be located using minutes as well.

Longitude is determined by time.  If you know what time it is in Greenwich, England, and what time it is in your present location, you can determine your longitude.  In the old days, ships used to carry two clocks – one standardized to Greenwich time, one set by the time at the current location (you can determine your current local time by setting your clock to 12:00 noon when the sun is highest in the sky).  Thus sailors could determine their longitude by comparing their local time with Greenwich mean time.  (Longitude is linked to time zones – we all know that when it is noon where we are, it is a different time at a place west or east of us).

  1. Great Circles and Small Circles
1b Great_circle_hemispheres

Great circles divide the earth in two equal parts

A concept related to latitude and longitude is that of great and small circles.  See 4CE Figure 1.17, p. 23 (3CE Figure 1.16, p. 22) – Great Circles and Small Circles.

a. “Great Circles” always cut the earth exactly in half; they must pass directly through the center of the earth:

  • for navigation (either sea or air), the shortest distance between two points always follows a great circle path
  • the only line of latitude that is a great circle is the equator.
  •  all lines of longitude are one half of a great circle.

b. “Small Circles” cut the earth into different sized pieces; they never pass through the exact center

  • all lines of latitude, except the equator, are small circles
  • no lines of longitude are small circles
  1. Meridians and Parallels (or circle of latitude)

Also related to latitude, longitude, great circles, and small circles are meridians and parallels.

a. “Meridians“ are halves of great circles, whose ends all meet at either the North or South Poles

  • meridians are the same as lines of longitude
  • all run in a true N-S direction
  • they are furthest apart at the Equator and converge at the Poles
  • an infinite number may be drawn; a meridian exists for any point on the globe

b. “Parallels“ are entire small circles of latitude parallel to the equator

  • parallels are the same as lines of latitude
  • they are all parallel (don’t diverge or converge)
  • they are all true E-W lines
  • they all intersect meridians at right angles
  • they are all small circles, except for the equator (the equator is a large circle)
  •  an infinite number may be drawn; a parallel exists for any point on the globe

So … latitude, parallels, and small circles are very closely related!  (remember, however, that the equator is a line of latitude, and a parallel, and a great circle!  All other lines of latitude are parallels, but also small circles)

And … longitude, great circles, and meridians are very closely related!  (remember, however that meridians and line of longitude are halves of great circles)

GPS, or Global Positioning System, is a technology that helps you locate a spot precisely, in terms of longitude, latitude, and elevation above sea level.  A series of satellites provide a triangulation network to help you locate any site exactly.  Most of us are very familiar with this in navigation systems we use in cars or carry with us.  Believe it or not, this technology has only been available wince 1994 (initially only for military use) — civilian use was only permitted in the late 1990s.

III, Maps and Map Projections

The ideal map or “model” of the Earth is a globe.  However small globes can include relatively little detail.  And detailed globes would have to be too large to be conveniently stored!

This creates a problem!  Unlike a cone or a cylinder, you cannot simply “unroll” a sphere, like the Earth, onto a flat piece of paper!  Try it!  You cannot lay out a spherical surface in any easy way.  Try cutting up a tennis ball … or the skin of a baseball … or an orange peel.  Try laying it out, flat, in a neat way.   It doesn’t work.  At least not in a way that would work well for a map!

To use mathematical terms, a sphere is not a “developable” surface.  4CE Figure 1.22, p.28 (3CE Figure 1.24, p. 28) – From Globe to Flat Map

Consequently, mapmakers (“cartographers”) have developed several “map projections”; mathematical attempts to put the spherical surface of the Earth onto flat pieces of paper.  Note that, because you cannot perfectly lay out a sphere on a flat paper, no map projection is perfect.  They are all distortions of reality!  But they are attempts to provide useful models of the Earth’s surface.

For a great introduction to map projections, check out Wikipedia on map projections.  The DGGS – Picture Gallery of Map Projections you could think of (and some you couldn’t!)

These are the most common map projections (see 4CE Figure 1.23, p. 29 (3CE Figure 1.25, p. 29) – Classes of Map Projections ):

  1. Cylindrical Projections try to picture the earth as if it were a tube or cylinder, rolled out (because you can actually unroll a cylinder … try it with the paper wrapper around your next can of beans) .  Of course the Earth is actually a sphere, so there will be distortions!

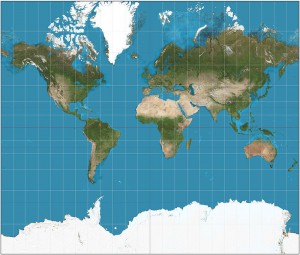1b 800px-Mercator_projection_SWThe most familiar cylindrical projection is the Mercator Projection (4CE Figure 1.23a, p. 29 (3CE Figure 1.25a, p. 29)).   On this projection:

– meridians do not converge as they really do (at 60° N & S, distances are exaggerated 2X; at 80° N & S, distances are exaggerated 6X.  Thus the Canadian Arctic and Greenland appear to be 6X as large as they really are!  They really aren’t that big!).  What the map makers have done is ADDED hundreds of square kilometers of land that don’t really exist, in the Arctic and Antarctic, to fill in the gaps)

– Mercator maps cannot show the actual North or South Poles (infinite exaggeration … notice how huge Antarctica seems to be on most maps … it’s not really that big!)

– the relative size, area, and shape of different locations is distorted (northern countries like Canada are exaggerated in size …  equatorial countries appear smaller than they are).  This is interesting.  We are used to Canada and Russia appearing SO huge!  They are big, but NOT actually as big as the appear!

– these maps excellent for navigational directions; a straight line drawn anywhere on the map is a line of constant compass bearing (called a rhumb line)  (4CE Figure 1.24, p. 29 (3CE Figure 1.26, p. 30)).  So, as a pilot, if you draw a straight line from Vancouver to London, it will give you the “lazy” route … you can fly along that line and never turn!  Note however this is NOT the shortest distance between Vancouver and London!

 – great circles (the shortest distances between places), however, appear as arcs.  These are terrible maps to try to determine the shortest distances between places.

  1. Planar or Azimuthal Projections try to simply lay out the earth on a flat plane. 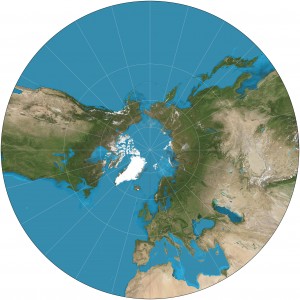 1b Gnomonic_projection_SWThe most interesting is the Gnomic Projection, because great circles (the shortest distances between points) are straight lines.  Thus planar projections are great for plotting air or sailing routes.  However rhumb lines (lines of constant compass bearing) appear as arcs.  (4CE Figure 1.23b, p. 29 (3CE Figure 1.25b, p. 29)).  So, when Air Canada plans its shortest route from Vancouver to London, they will use a gnomic projection.  It will give the shortest distance.  It is NOT the easiest route to fly however, because the pilot will have to constantly adjust his compass direction.  However, most maps in the airlines’ magazines are variations of Mercator projections … so in the in-flight magazine, flight routes usually appear as arcs.
  1. Conic Projections try to picture the earth as a cone.  1b USGS_map_Albers_conic_tallBy combining a series of conic sections to create a “polyconic” projection, distortion is minimized.  This is the best projection for showing limited portions of the Earth as accurately (with the least amount of distortion) as possible).  However global conic projections — when you try to use them for a large area, like the whole Earth — look very odd!.  4CE Figure 1.23c, p. 29 (3CE Figure 1.25c, p. 29).  These are great projections for highway maps of Alberta, even of Canada or the U.S.

Maps are fascinating things for all sorts of political reasons, too!  The projections we use influence how we see the world.  In the Mercator Projection, for instance, northern areas are enlarged, relative to equatorial areas.  Canada and Russia appear huge!  In fact, Canada is not that much bigger than Brazil!  There are other ways to view the world!

1b upside_down_3For instance, most of our maps have “north” at the top.  This is not necessary!    Australian cartographers have argued we should put “south” at the top.  Check out the results:   Upside Down Map Page  

  • Note that Europe and North America are no longer the first places you notice … Africa and South America are.  Interesting …  Some scholars point out that by putting North America and Europe in the top centre of virtually every world map, we have subconsciously suggested that these are the most important regions of the world.  It would be interesting to redraw maps with other continents front and centre.  How might that change our perspective on the world?
  • What happens when North America is “maraginalized” (lower left), and Australia is front and centre?
  • What happens to your perspective on the world when Africa is front and centre?

As Christians with a heart for poorer nations, our perspective on the world is worth some reflection …  There are other ways of “seeing the world” than centered on Europe and North America.  When we see Canada marginalized, how do we feel?  Would you dare use an “Upside-Down Map” on your church’s “Mission Bulletin Board”?  Why?  Why not?

Another interesting projection is this one, centred on New Zealand, rather than the United Kingdom.  Notice how “marginalized Canada is now?

Aside:  Map Making … or cartography (you don’t need to study this)

From the Natural Resources Canada:

Early European explorers of this country’s vast geography made maps using a variety of instruments, from compasses to survey chains. Cartography, the science of mapping, is now high-tech.

Cadastral or legal surveyors measure and establish property boundaries and other land rights in the form of cadastral parcels. Using modern mapping technology, the Legal Surveys Division of Natural Resources Canada creates and maintains digital parcel mapping information on Canada Lands. Canada Lands include First Nation Lands, National Parks, the territories and the off-shore areas of Canada. As well, the International Boundary Commission, as part of this group, maintains the 8,891 kilometre-long U.S./Canada border.
Measuring and surveying the countryside is the first step in making a map. Today surveyors often rely on global positioning system (GPS) to pinpoint the latitude, longitude and elevation of any where on earth. Commonly used GPS receivers read transmissions from orbiting satellites to get an accuracy of +/- 100 meters. When combined with other special techniques, an accurate reading to within centimetres can be reached.
Geodesy is the science of locating and relating the position of objects on the earth and in relation to each other. It all begins with a fixed reference point, and the most stable non-moving object in the universe is a deep space quasars. The Geodetic Survey Division uses the position of quasar, plus GPS satellite tracking stations, to set up a network of permanent reference points which are linked together to make a reference framework. These framework points, or coordinates, are the fundamental skeleton which allows surveys, maps, images and other digital information to fit together when a map is made.
Topographic Maps accurately show the topography, or terrain features of an area. This includes mountains, hills, valleys and plains. Topographic maps also show hydrographic features, such as lakes, rivers and streams. Many features built by people are shown on the maps, such as cities and towns, schools, buildings, roads, railways and power lines. Since they are very detailed, topographic maps are useful for recreational activities like canoeing, fishing, hiking, orienteering and snowmobiling. They are also used by governments and industries to respond to emergencies, manage natural resources and study the environment.
National Topographic System of Canada divides the entire country into a grid of individual topographic map sheets, determined by the area’s latitude and longitude. They come in two scales, 1:250,000 and 1:50,000. A 1:250,000 scale map covers a large area with a medium level of detail, while a 1:50,000 scale map has more geographic detail, but covers a smaller area. Natural Resources Canada’s topographic maps are available both on paper and on CD-ROM.
To make maps Canada has been photographed from the air for over 70 years. Every square kilometre of country has now been photographed and many areas have been re-photographed several times. Aerial photographs have been used by the federal government to produce topographic maps through a process called “stereo-compilation”. Aerial photos are also used for environmental assessment, urban planning and for land claims. Over six million aerial photographs are archived at the National Air Photo Library in Ottawa, and are available to the public.
When a geographic area is very remote Canada’s RADARSAT satellite takes remote sensing images and collects data for map makers. The Canada Centre for Remote Sensing uses earth observation satellite information for many other things, such as monitoring crops, vegetation and forest fires. RADARSAT 2, with state-of-the-art Canadian systems and technologies, was launched in 2001.
Toponyms, or geographical names, are added to maps to identify landscape features. They may sometimes also reveal interesting things about the local history of an area. In Canada, place names on official maps must be authorized through the Geographical Names Board of Canada.
Computers and Geographic Information Systems (GIS) software bring together the diverse data from surveys, position readings, aerial photographs, satellite images and geographical names to make a map. The information is layered on top of each using the geodetic framework to help them fit together properly. Titles, legends and other cartographic information are then added to make a map. Although many of the resulting maps are still printed on paper, digital maps are now very popular. Most of the maps produced by Natural Resources Canada are available in either format.
For over one hundred years, the National Atlas of Canada has described Canada’s physical, economic and social geography with a collection of maps, graphs and tables. The Atlas’s sixth edition is now available entirely on the Internet, where users can view and download up-to-date maps, build their own maps, and have access to a wide variety of related information services. Classes can even join the Canadian Communities Atlas network of schools.

An interesting read:

“The modern map is no longer an unwieldy printed publication we wrestle with on some blustery peak, but digital, data-rich, and dynamic.  It is transforming the way we interact with the world around us.  Thanks to “big data”, satellite navigation, GPS-enabled smartphones, social networking and 3D visualisation technology, maps are becoming almost unlimited in their functionality, and capable of incorporating real-time updates.  Advanced LED screen technology and smartphones equipped with projectors are going to transform the way we interact with maps,” says Ian White, founder and chief executive of Urbanmapping.com, a San Francisco-based geoservices provider.  For example, tourists will be able to plan their visits by using their phones to project a 3D map onto a wall, that they’ll then be able to manipulate it remotely with their hands, adding layers of information such as landmarks, restaurants, recommendations from friends, as well as transport links and times …”  continue reading here:  BBC News – The maps transforming how we interact with the world

IV. Remote Sensing and Geographic Information Systems (GIS)

Remote sensing is a means of gathering information about an object (like the Earth) without direct physical contact. We “remote sense” all the time – with our eyes, our nose, cameras, binoculars, telescopes, etc.

Active remote sensing involves sending something out – a probe to Mars, sonar beams, radar beams, drones with cameras, etc. – and monitoring the results.

Passive remote sensing involves observing an object without sending anything – taking a picture, recording seismic waves after an earthquake, monitoring solar radiation.

Geographic Information Systems (GIS) refer to computer-generated data bases that combine many layers of data (often gathered by remote sensing) – both natural and human – for a particular location so that their relationships and interconnectedness can be studied and modeled.  GIS models help to show the potential environmental or other effects possible when changes are introduced into a location.  See GIS.com – the Guide to Geographic Information Systems for a complete introduction!

For example, a GIS model of the changes associated with a new highway overpass would show human changes like road alignment, traffic flow, zoning, land ownership, etc, and natural changes like drainage patterns, vegetation changes, wildlife habitat and migration, etc.

GIS models are used extensively in environmental impact assessments associated with major development projects.  They can also be used to evaluate natural hazards and alert people of past, present and future risks.  In the U.S., for instance, you can enter the name of your community and generate a map that shows your flood hazard, earthquake activity, hurricane activity, hail storms, wind storms, or tornadoes … neatly layered GIS data!

Toporama is a Government of Canada programme that allows you to view multiple layers of information for anywhere in Canada.

More and more GIS information is being posted on the web daily — it’s the cutting edge these days — check out your community’s GIS presence online.  In many ways Google Earth (have you found yourself yet?) and Google Maps are a simplified GIS product — layering maps, satellite images, etc.

There is a great YouTube video on how digital mapping is changing our perspectives on the world from Penn State University:  http://www.youtube.com/watch?v=ZdQjc30YPOk&feature=player_embedded

Because Canada has so much land area – much of it uninhabited, but rich in resources – Canadians have been among the world leaders in remote sensing and GIS technologies!  If you want a career tip … check out GIS.  It is one of the booming employment sectors!

.

Worth reflecting on …
Please watch these two short interviews with Dr. Jennifer Wiseman, head of NASA’s Space Telescope Programme.  Dr. Wiseman is an amazing scientist and a strong Christian!  You will be encouraged!

Jennifer Wiseman – Personal Story [1] – YouTube

Jennifer Wiseman – Personal Story [2] – YouTube

Feel free to discuss the interviews on the course discussion site (see the syllabus for details …)

 

Do not worry about time zones … although this may be interesting to you, you don’t need to know it for this course!

This page is the intellectual property of the author, Bruce Martin, and is copyrighted by Bruce Martin.  This page may be copied or printed only for educational purposes by students registered in courses taught by Dr. Bruce Martin.  Any other use constitutes a criminal offence.

Scripture quotations marked (NLT) are taken from the Holy Bible, New Living Translation, copyright © 1996. Used by permission of Tyndale House Publishers, Inc., Wheaton, Illinois 60189. All rights reserved.

Mercator projection:  “Mercator projection SW” by Strebe – Own work. Licensed under CC BY-SA 3.0 via Commons – https://commons.wikimedia.org/wiki/File:Mercator_projection_SW.jpg#/media/File:Mercator_projection_SW.jpg

Great circle:  “Great circle hemispheres” by Jhbdel at en.wikipedia. Licensed under CC BY-SA 3.0 via Commons – https://commons.wikimedia.org/wiki/File:Great_circle_hemispheres.png#/media/File:Great_circle_hemispheres.png

Upside down map:  http://www.mapworld.com.au/products/upside-down-world

Latitude-longitude:  Illinois State University